Liquid coatings on curved substrates
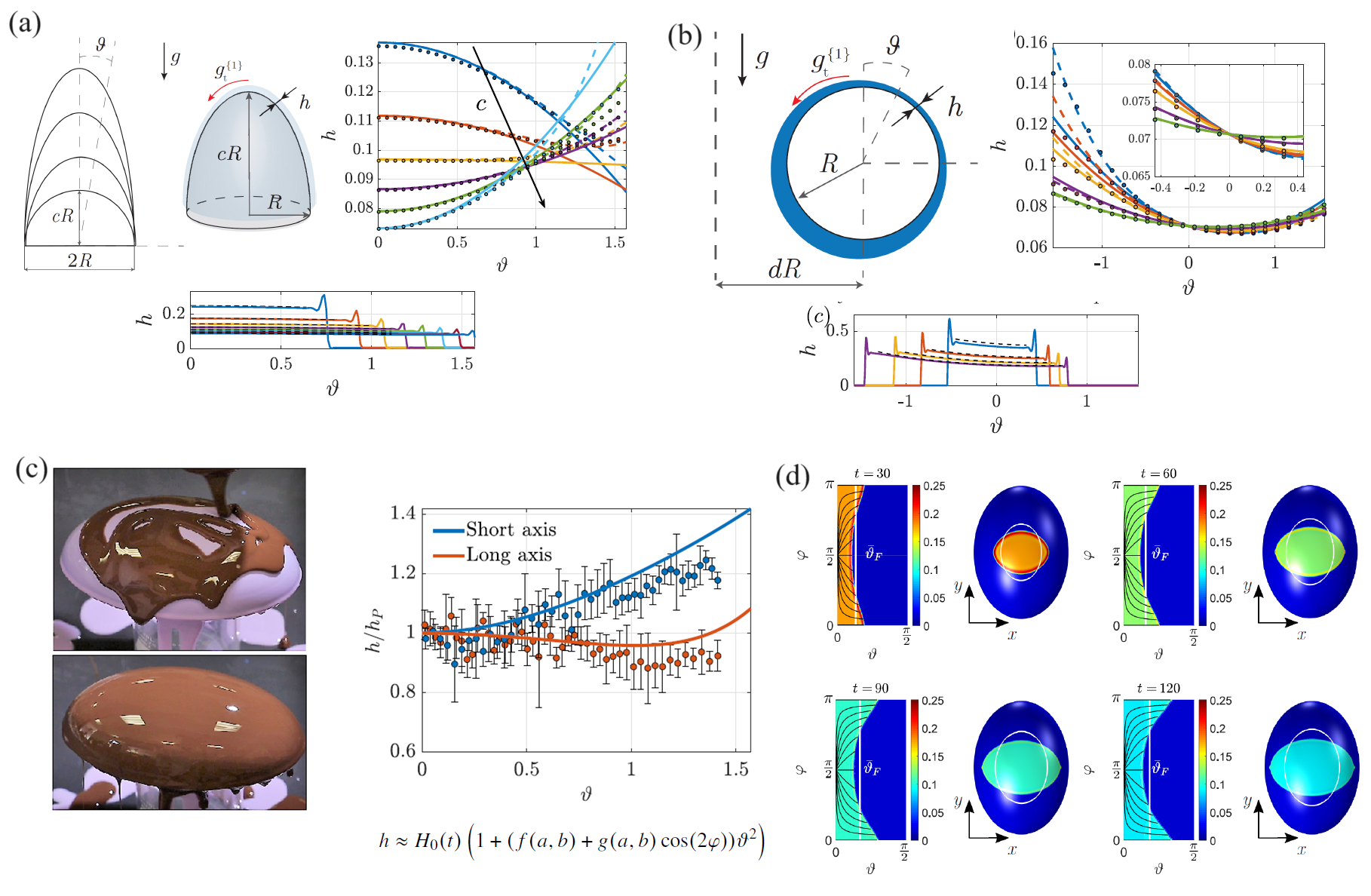
The art and science of applying coatings to various materials have evolved over millennia, leaving an indelible mark on diverse fields such as architecture, industry, and art. Imagine you spill a drop of honey on different surfaces, like a curved bowl or a flat table. Although the drainage and spreading processes of thin liquid films on substrates have received growing attention during the last decades, the three-dimensional analysis of coating flows on surfaces is limited to flat and axisymmetric substrates. Here, in collaboration with the research group of Prof. P-T Brun (Princeton University) and Prof. M. Pezzulla (AArhus University), we exploit differential geometry to study the drainage and spreading of thin films on generic curved substrates. Using the lubrication approximation, we initially investigate the drainage and spreading processes on spheroidal and paraboloidal substrates by employing an asymptotic expansion in the vicinity of the pole and a self-similar approach, finding that the thickness distribution is set by the substrate metric and tangential gravity force components. Spheroids with a large (small) ratio between height and equatorial radius are characterized by an increasing (decreasing) thickness moving away from the pole. The non-symmetric coating on a toroidal substrate shows that larger thicknesses and a faster spreading are attained on the inner region than on the outer region of the torus. An ellipsoid with three different axes is chosen as a testing ground for three-dimensional drainage and spreading. Modulations of the drainage solution along the azimuthal direction are observed, with a variation of the thickness along both axes. We derive an analytical three-dimensional solution which well agrees with numerical results. By imposing the conservation of mass, an analytical solution for the average spreading front is obtained. The analytical and numerical results are in good agreement. The resulting drainage solutions show also a favorable agreement with experimental measurements obtained from the coating of a curing polymer on diverse substrates.